Cada vez los problemas se vuelven más complejos, no tenía idea; pero aquí seguimos sin tirar la toalla. Este problema en especial me pareció interesante y me gustaría resguardarlo e incluso compartirlo.
Enunciado - Day 5: Hydrothermal Venture
Voy a tratar de resumirlo, pero todo está en el siguiente link:
Consiste en una n cantidad de líneas cada una definida por 2 puntos y debes calcular cuántas veces se encuentran entre sí.
Si tienes unos líneas como estas:

El resultado debe ser el siguiente, donde los 2 son los lugares que se encuentran las rectas. El resultado solo es la cantidad de veces que se encuentran las líneas, es decir 5.

Yo me quedé hasta la parte 1, que son horizontales y verticales (por el momento)
Planteando las Bases
Uno de los puntos que define el enunciado es que te imagines en el ejemplo es algo como esto (es idéntico a los gráficos en una pantalla):
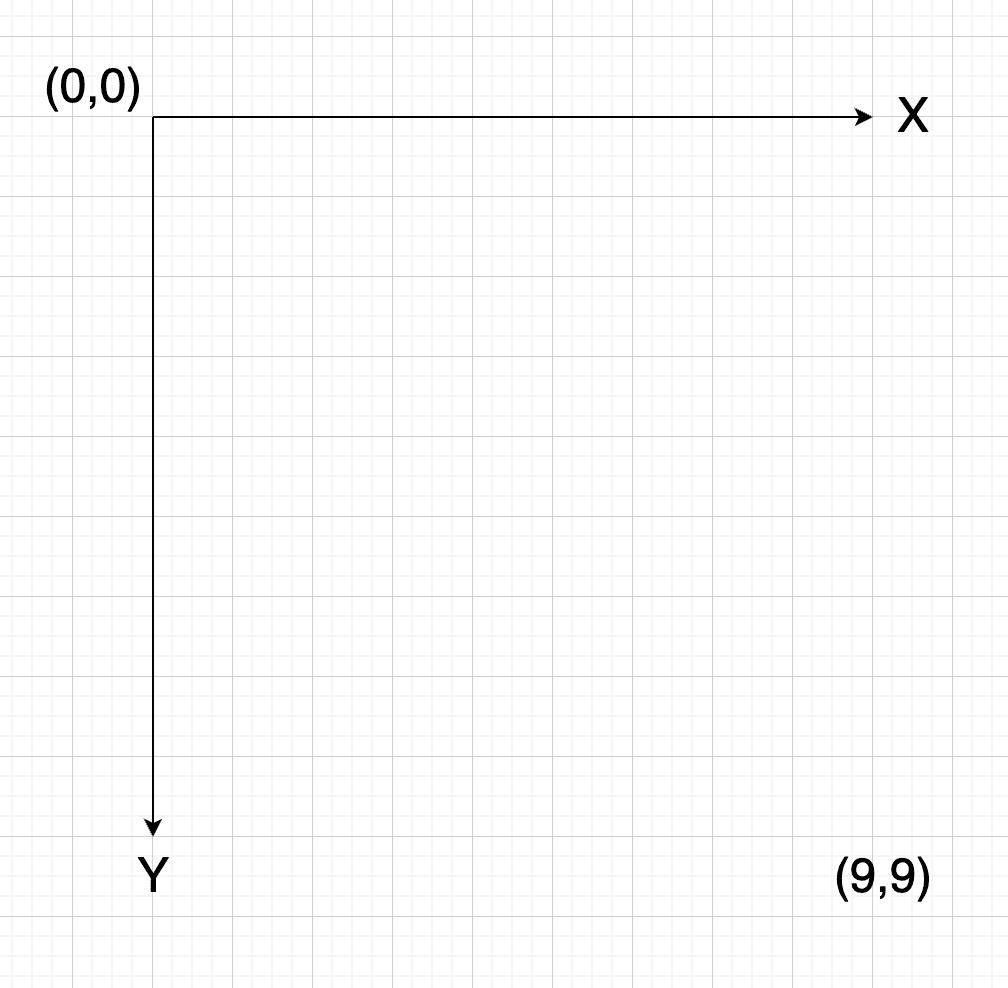
Sin dar muchas vueltas seguro dirás que son rectas; pero realmente son "segmentos de una recta" y esto es muy importante. Ejemplo, digamos que quiero representar (7,0 -> 7,10).
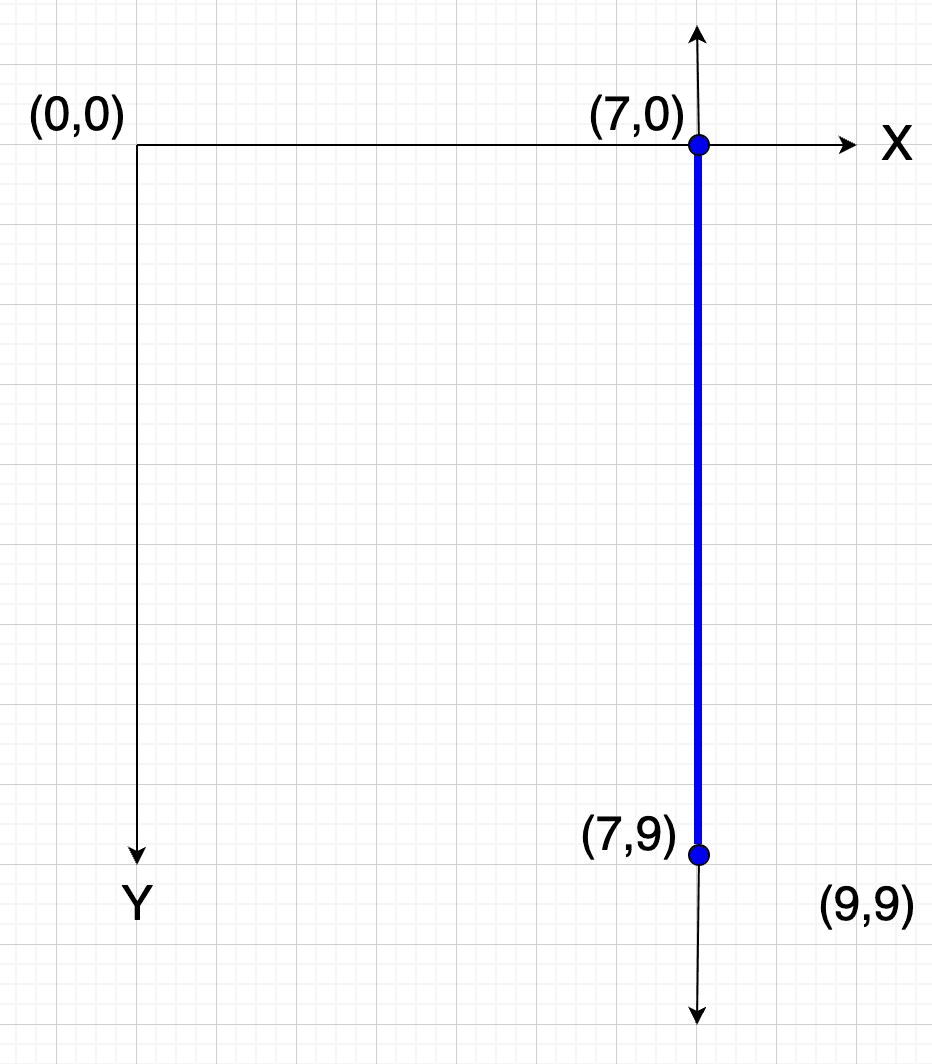
Como puedes apreciar lo azul es realmente un segmento (un segmento rectilíneo) y la línea negra detrás de él es la representación de una real recta vertical.
De igual forma podemos apreciar que al tratarse de verticales y horizontales, hay una coordenada que siempre persiste; en el caso del ejemplo, es la X y se puede representar por una ecuación: x = 7
Metiendole un poquito de análisis, podemos ver:
Verticales -> X = constante
Horizontales -> Y = constante
Es decir que lo primero que podemos filtrar en el algoritmo es:
Si X1 = X2 -> esta linea es vertical
Si Y1 = Y2 -> esta linea es horizontal
Casos posibles
Ya tengo mis datos listos para ser analizados, necesito saber cuales son los casos en que se encuentran o intersectan, hay 2 casos:
-
Un segmento horizontal vs vertical
- Se encuentra el segmento horizontal y el segmento vertical
- No se encuentra el segmento horizontal y el segmento vertical
-
Un segmento sobre la misma recta (ya sea horizontal o vertical)
- Se encuentra el segmento dentro del otro segmento
- Empieza el segmento fuera del otro segmento y se encuentra al final
- El segmento empieza dentro del otro segmento
- No se encuentran ambos segmentos
Un Segmento Horizontal vs Vertical
Digamos que yo tengo este caso:
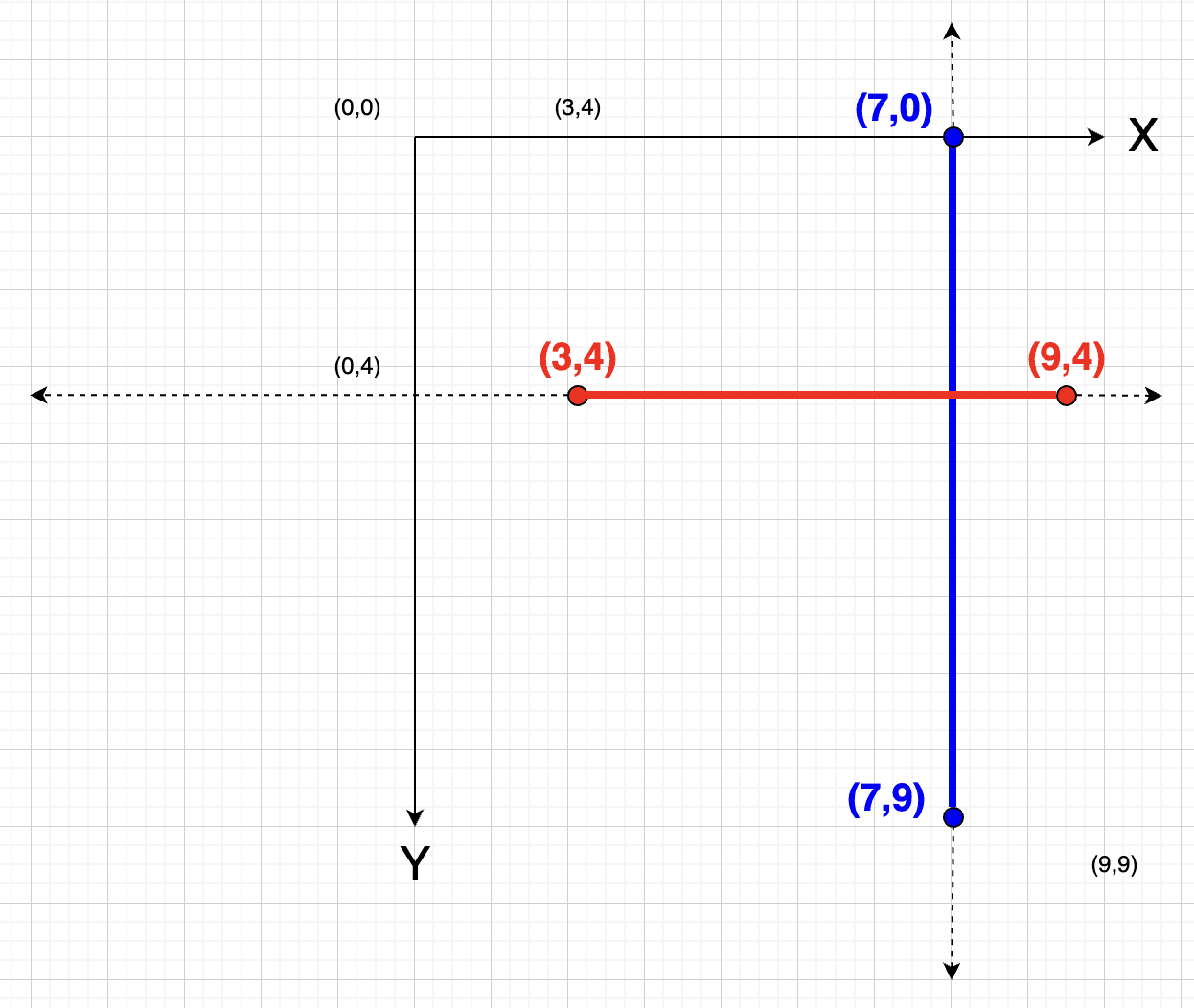
Si yo se que en todos sus puntos la linea azul será X = 7 y en todos los puntos de la línea roja Y = 4, el punto en que se están tocando ambos segmentos es (7,4). Esto lo sé, porque sus líneas pasan justo por ahí.
Pero esto no es tan sencillo como parece, ¿qué pasa si no se tocan ambos segmentos?
¿Cómo determino si interseccionan los segmentos?
Digamos que tengo el siguiente caso:
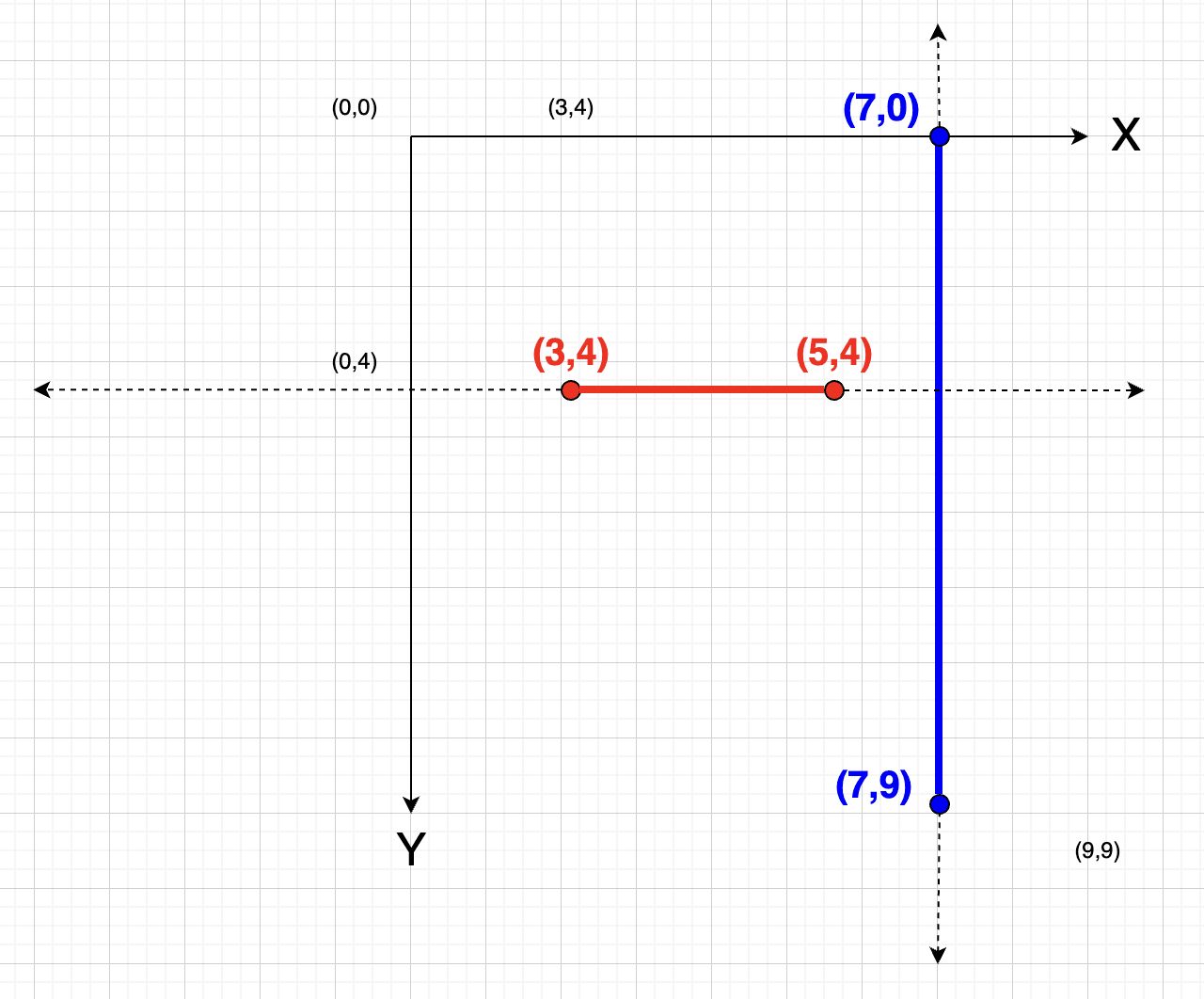
Si se donde "podrían intersectarse" los segmentos si fueran rectas, puedo revisar si ese punto se podría estar dentro de uno de los segmentos. Por ejemplo:
¿El punto (7,4) podría estar dentro del segmento (3,4) -> (5,4) ?
¡No, 7 no está dentro del rango de 3 -> 5!
Un segmento sobre la misma recta
Hay multiples casos que pueden ocurrir, como expliqué anteriormente; pero todo se reduce a una verificación, pero veamos los casos paso a paso:
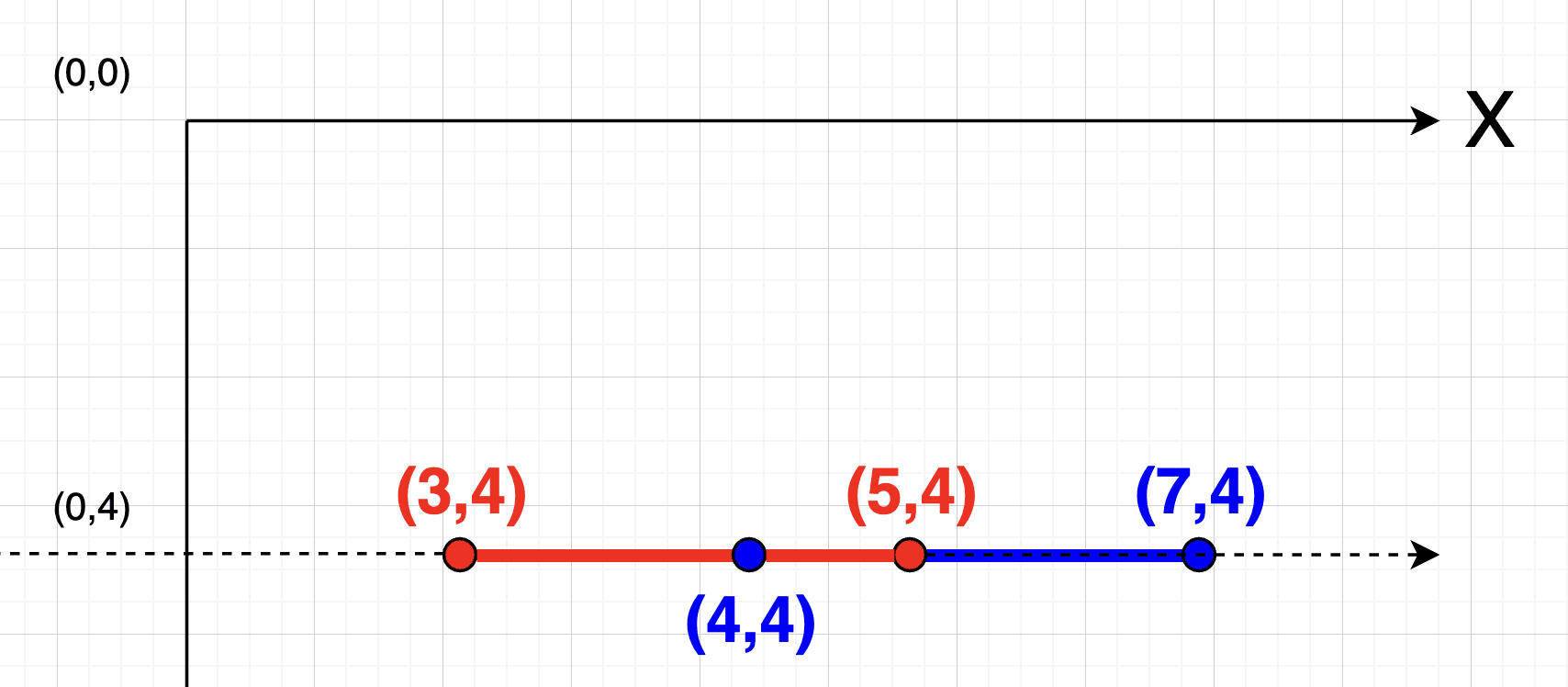
Aquí los segmentos se tocan desde el 4,4 hasta el 5,4.
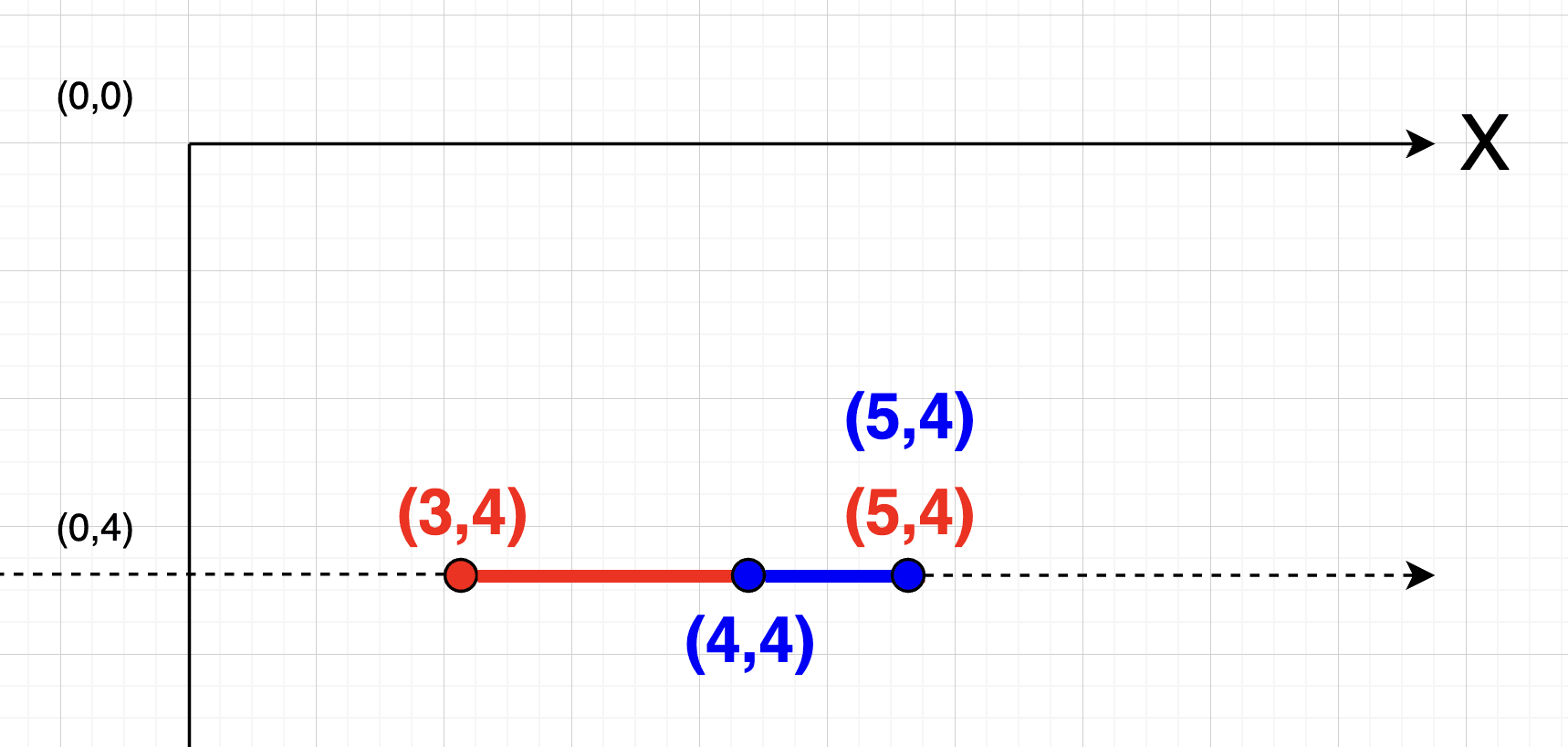
Aquí los segmentos se tocan denuevo desde el 4,4 hasta el 5,4, pero como puedes apreciar uno está dentro del otro.
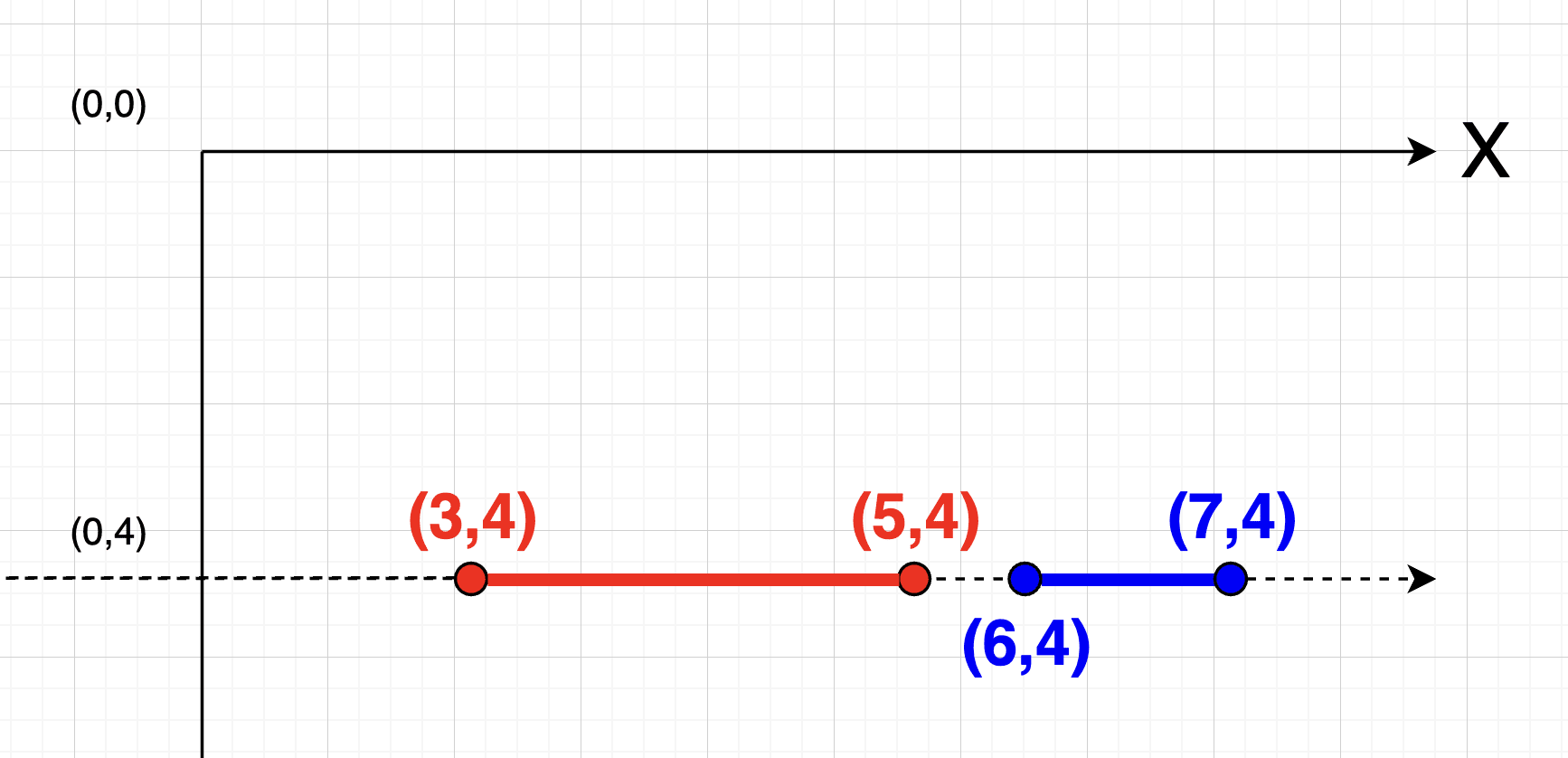
Por último, los segmentos no se tocan en ningun punto, esto quiere decir que debemos seguir verificando la intersección.
Ya este último se verificaría revisando si ambos puntos de ambos segmentos podrían estar dentro del otro segmento, como mostré en la sección anterior.
Concentrándome en los casos en que sí se intersectan y se encuentran en múltiples puntos, ¡debemos trabajar esto con rangos!
Utilizando Rangos
Volvamos al primer ejemplo:
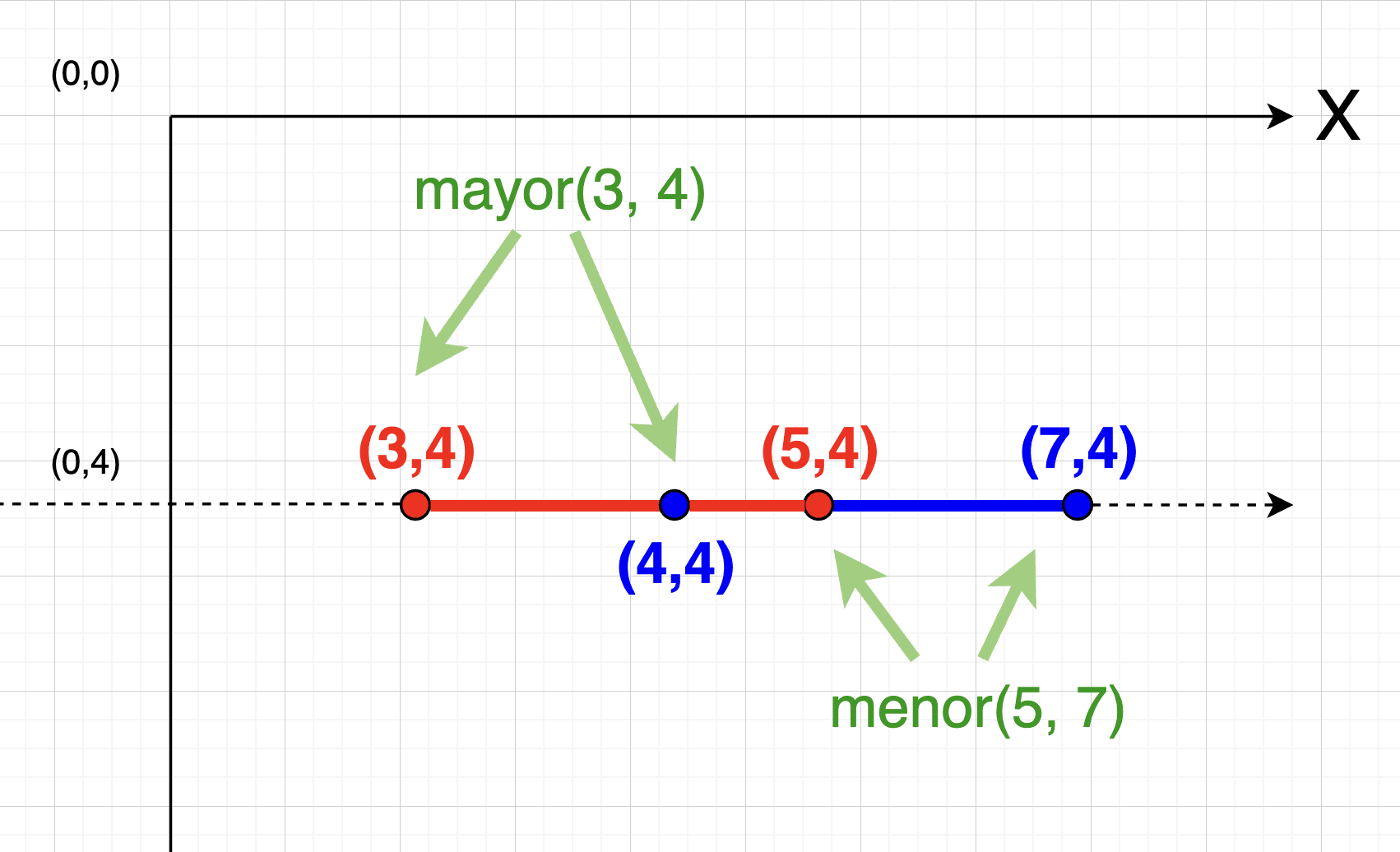
L1 = (3,4) -> (5,4) L2 = (4,4) -> (7,4)
El mayor entre 3 y 4 es 4 y el menor entre 5 y 7 es 5. Por lo tanto solo debo encontrar los puntos dentro de ese rango, un loop hasta el otro extremo.
Detallitos
El problema tiene valores de entrada de segmentos dirigiendose hacia la izquierda o a la derecha, por lo tanto debí ajustar todos los segmentos hacia un solo sentido (la derecha).
Al momento que publico este análisis, no tengo el algoritmo listo (está el antiguo de hecho); pero pronto lo estará y si encuentro algún otro punto no dudaré en agregarlo acá:






